Rで局所回帰(LOESS)を実行する

R
Published

December 10, 2024

RでLOESS (locally estimated scatterplot smoothing) による局所回帰を実行する方法のメモです。 LOESSによる局所回帰は、ざっくりというと、点を曲線で回帰する方法です。 直線ではなく曲線で回帰線がかけそうなときに使えます。

使用するデータセット

今回はmtcarsデータセットを用いて試してみます。 str関数で中身をのぞいてみます。

str(mtcars)
'data.frame':   32 obs. of  11 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
 $ disp: num  160 160 108 258 360 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ qsec: num  16.5 17 18.6 19.4 17 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

自動車のスペックのデータが入っています。 詳しくはhelp(mtcars)もしくは?mtcarsでドキュメンを開いて読みます。

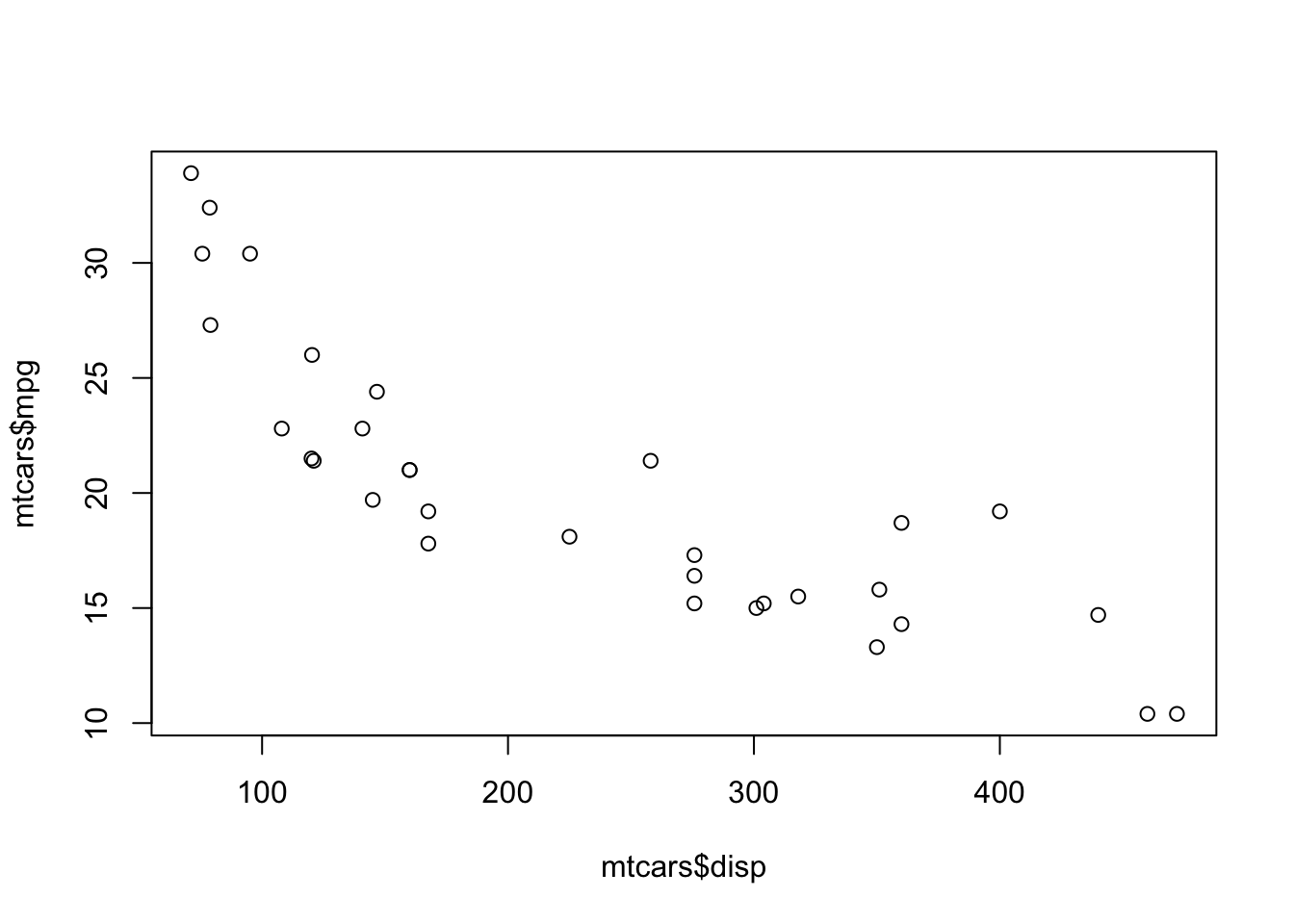
今回は、エンジン排気量dispと燃費mpgの関係を見てみます。 とりあえずプロットしてみます。

plot(mtcars$disp, mtcars$mpg)

直線というよりは、右下がりの曲線が引けそうですね。

LOESSモデルの作成

LOESSモデルを作成して回帰線を引いてみます。 LOESSモデルはloess関数で作成できます。 基本的には、loess(応答変数 ~ 説明変数, data = データフレーム名)と書きます。

model <- loess(mpg ~ disp, data = mtcars)

適当にモデルをのぞいてみます。

print(model)
Call:
loess(formula = mpg ~ disp, data = mtcars)

Number of Observations: 32 
Equivalent Number of Parameters: 4.24 
Residual Standard Error: 2.295

よくわかりませんね。

回帰線を描画する

中身はよくわからないので、とりあえず回帰線を描いてみます。 回帰線はpredict関数で簡単に作成できます。 predict(モデル)が基本的な書き方です。

prediction <- predict(model)
print(prediction)
 [1] 20.12337 20.12337 25.75360 17.33610 15.40363 17.86670 15.40363 21.20958
 [9] 21.78554 19.58765 19.58765 16.67062 16.67062 16.67062 11.75730 12.26543
[17] 13.03809 30.45157 30.99716 31.85873 24.12662 16.15084 16.32958 15.61758
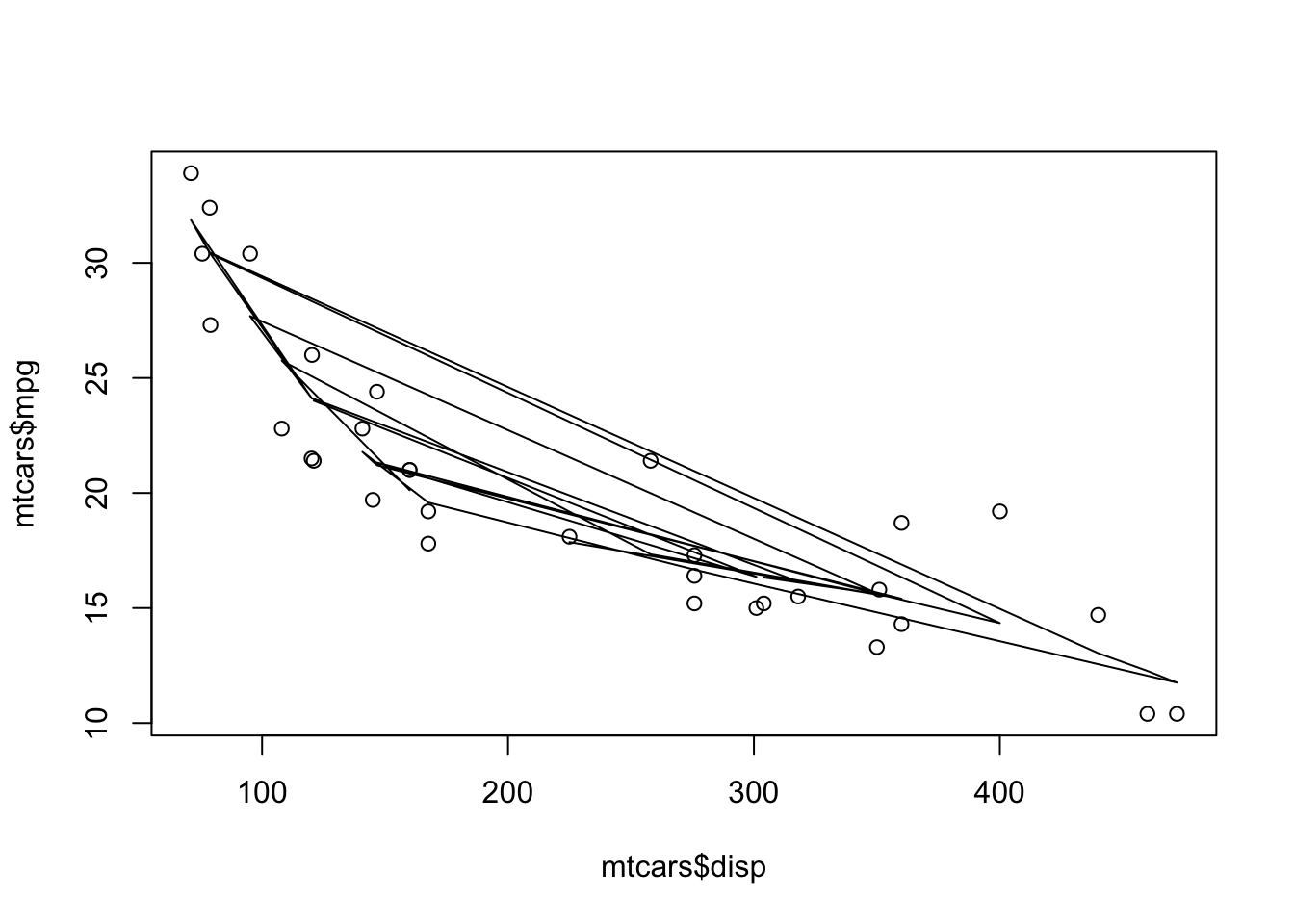
[25] 14.34416 30.39788 24.10123 27.68788 15.59833 21.37202 16.35572 24.01281

それぞれの点(dispの値)に対して予測値が算出されます。 そのままプロットの上にlines関数で線を引いてみます。

plot(mtcars$disp, mtcars$mpg)
lines(mtcars$disp, prediction)

ぐちゃぐちゃでよくわからないですね。 これは、lines関数が与えられたベクトルの順番に線を引いていくためです。 つまり左から右に向かって線を引くには、、dispを昇順(小さい方から大きい方)でならべる必要があります。 dispと予測値predictionを結合させてデータフレームを作成し、その後並び替えてもよいですがpredict関数を実行する際に昇順でデータフレームを作成することができます。 このためには、predict関数の引数newdataに説明変数を入れたデータフレームを指定します。 今回の場合は、dispをsort関数で昇順で並び替えたデータフレームを与え、その値に対してpredict関数で予測したデータフレームを作成します。

prediction <- predict(model, newdata = data.frame(disp = sort(mtcars$disp)))

newdataとして与えるデータフレームの列名は説明変数と同じにします。 今回の場合はモデルにdispを与えたので、列名をdispとして名前を揃えます。

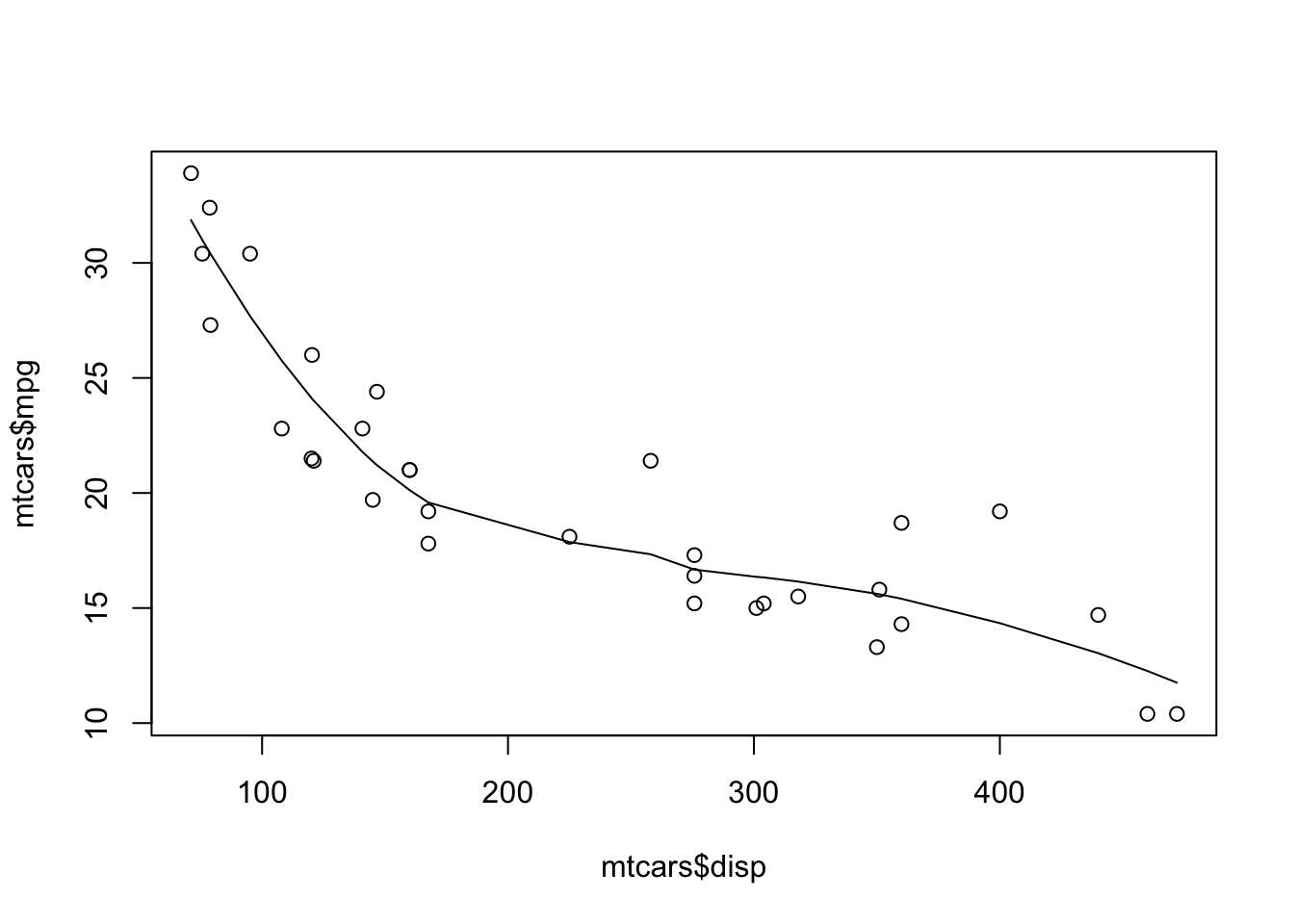
その後、今一度回帰線を引いてみます。 lines関数のx座標の値もsort関数でdispを昇順にしたものを与えるのを忘れないようにします。

plot(mtcars$disp, mtcars$mpg)
lines(sort(mtcars$disp), prediction)

良い感じの線が引けました。

95%信頼区間を描画する

これで終わりでももちろん良いですが、せっかくなので95%信頼区間もつけてみます。 詳細は省きますが、95%信頼区間は\(予測値 \pm 1.96 \times 標準誤差\)となります。 標準誤差 (standard error, SE)はpredict関数で予測する際に、se = TRUEとすることで算出できます。

prediction <- predict(model, newdata = data.frame(disp = sort(mtcars$disp)), se = TRUE)
str(prediction)
List of 4
 $ fit           : Named num [1:32] 31.9 31 30.5 30.4 27.7 ...
  ..- attr(*, "names")= chr [1:32] "1" "2" "3" "4" ...
 $ se.fit        : Named num [1:32] 1.142 1.037 0.974 0.968 0.712 ...
  ..- attr(*, "names")= chr [1:32] "1" "2" "3" "4" ...
 $ residual.scale: num 2.3
 $ df            : num 27.3

この場合は、リストが返ってきて、fitに予測値、se.fitに標準誤差がそれぞれ入っています。 信頼区間描画用のデータフレームd_predictを作成してみます。

d_predict <- data.frame(x = sort(mtcars$disp), 
                        fit = prediction$fit, 
                        upper = prediction$fit + 1.96 * prediction$se.fit,
                        lower = prediction$fit - 1.96 * prediction$se.fit
                        )

見やすさのために改行を入れていますが、なくても大丈夫です。 upperが信頼区間の上側、lowerが下側になります。 描画の順番に気をつけて、信頼区間、生データ、回帰線となるようにプロットを作成します。 信頼区間はpolygon関数で塗りつぶします。

plot(mtcars$disp, mtcars$mpg, type = "n")
polygon(c(d_predict$x, rev(d_predict$x)), 
        c(d_predict$lower, rev(d_predict$upper)), 
        col = "gray", border = NA)
points(mtcars$disp, mtcars$mpg)
lines(d_predict$x, d_predict$fit)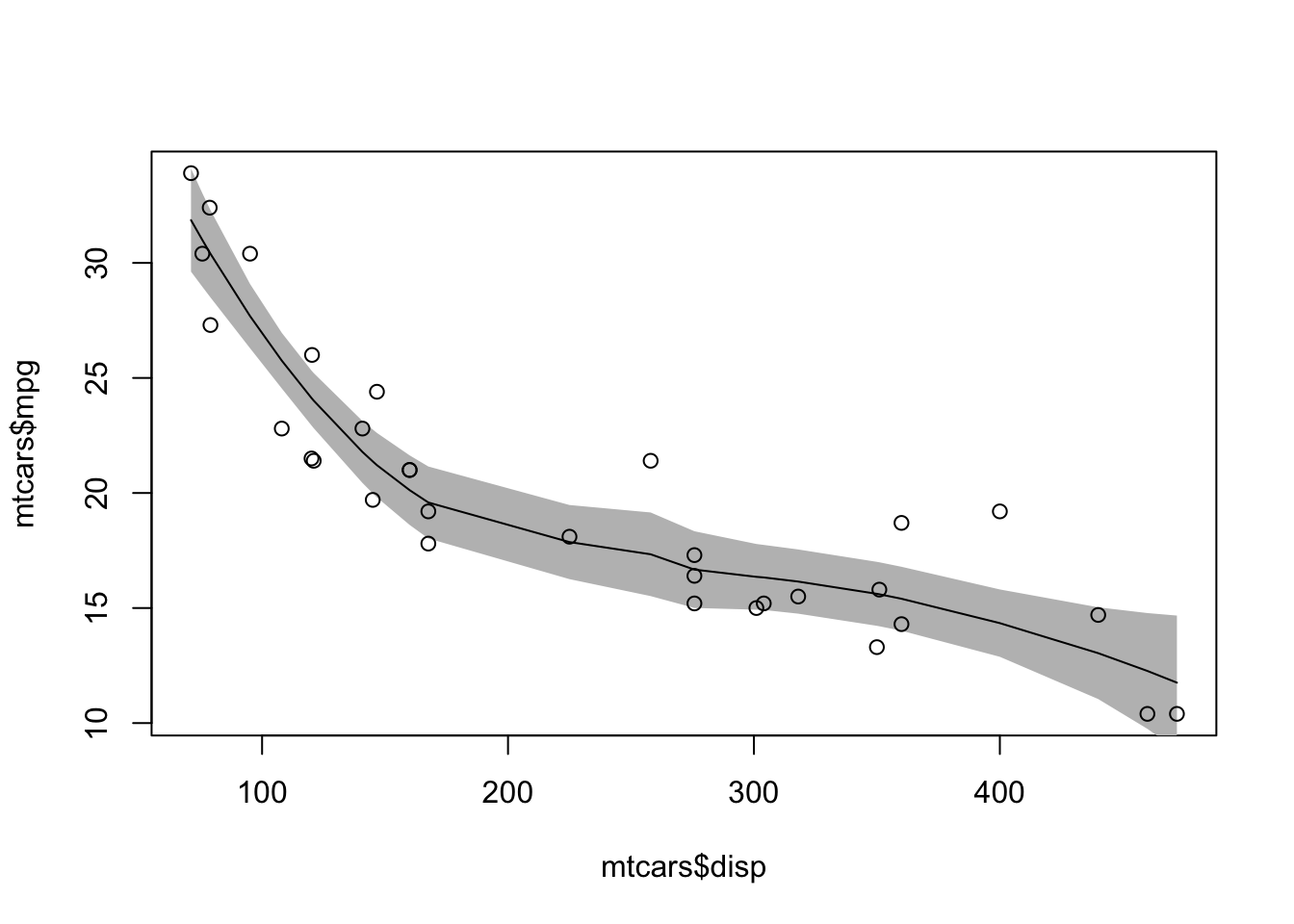

polygon関数は所見ではややこしい部分です。 linesと同じように、与えられた順番に頂点を取り、頂点で囲まれた部分を塗りつぶします。 そのため、x座標は、左端から右端までいって、逆順に右端から左端に戻ります。 y座標は信頼区間下側からいって、上側から戻ってきます。 ベクトルの順番を逆にするためにrev関数を使用しています。 また、境界線があると回帰線と混同してしまうため、border = NAとして描画しないようにします。

必要に応じて回帰線を太くしたり(lines関数内のlwd)、色を変えたり(col)、透過させたり(colをカラーコードで指定し、末尾に透過度を書く)などのカスタムが可能です。

その他

  • 予測がうまくいかない場合は、loess関数内のspan引数を変えてみます
  • 欠損値NAに対する処理はloess関数内のna.actionで設定します
    • NAも含める場合はna.pass
    • NAを省く場合はna.omit
Back to top