決定係数\(R^2\)をRで計算する方法をまとめます。
\[ R^2 = \frac{予測値の偏差平方和}{実測値の偏差平方和} \]
偏差は値から平均値を差し引いた値のことなので、偏差平方和\(\mathrm{SS}\)は測定値を\(x\)として、平均値を\(\overline{x}\)とすると、以下の式で計算されます。
\[ \sum^n_{i=1} = \left( x_i - \overline{x}_i \right) ^2 \]
つまり、予測値を\(\widehat{x}\)として、\(R^2\)を数学的に表すと、以下のようになります。
\[ R^2 = \frac{\sum^n_{i=1}\left( \widehat{x}_i - \overline{x}_i \right) ^2}{\sum^n_{i=1} \left( x_i - \overline{x}_i \right) ^2} \]
感覚的な理解としては、偏差平方和が平均からのズレ、言いかえるとデータのばらつきなので、分母が全体のばらつき、分子が回帰モデルによる予測値のデータのばらつきということになります。 つまり、\(R^2\)は予測したデータのばらつきが全体のばらつきをどのくらい表せているかの指標と言えます。
mtcarsというデータセットを例にして\(R^2\)を算出してみます。 これは車の性能についてのデータセットで、32台の車について11個の測定項目(変数)があります。 燃費mpgはエンジンの排気量dispによってどの程度説明されるでしょうか?
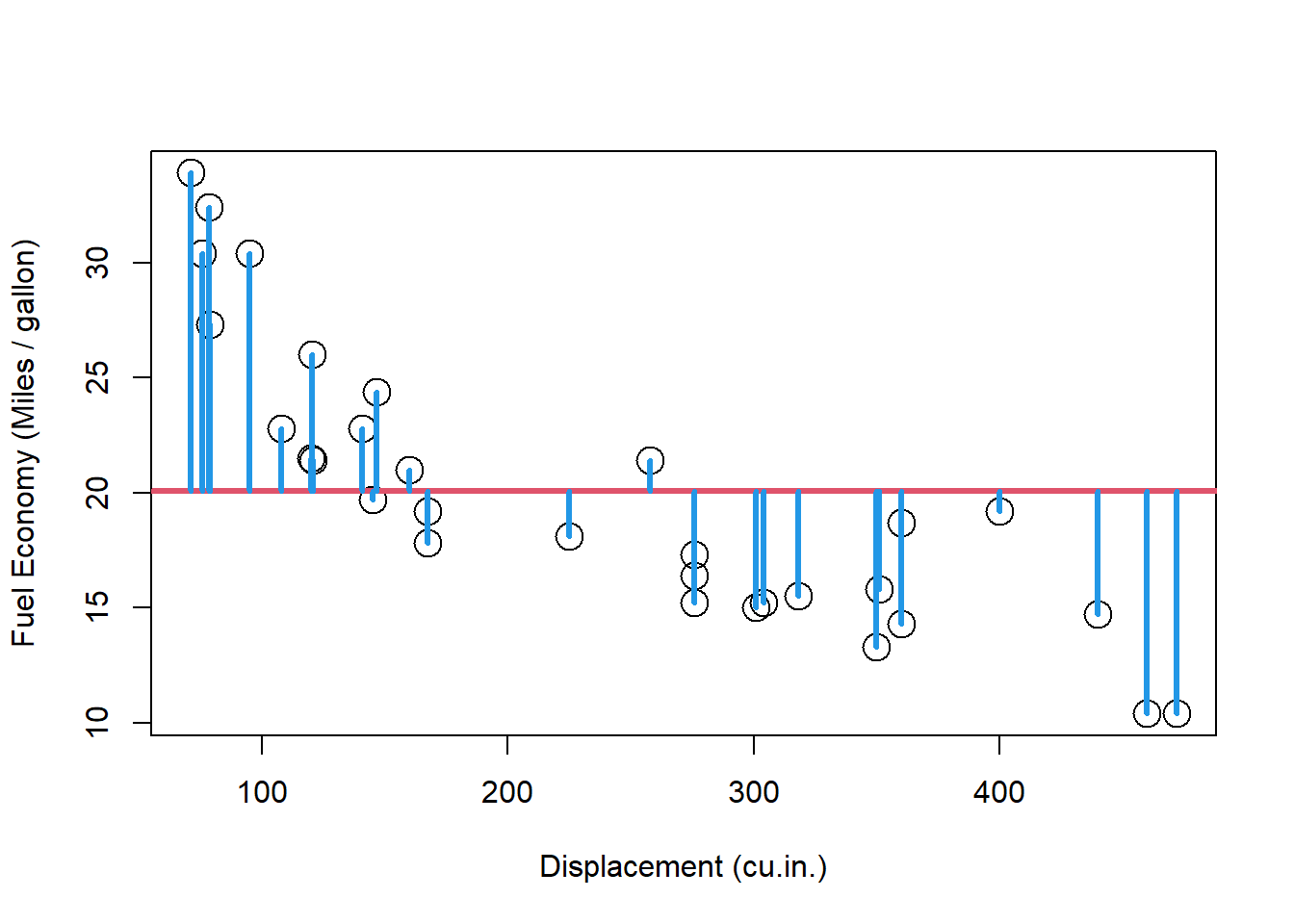
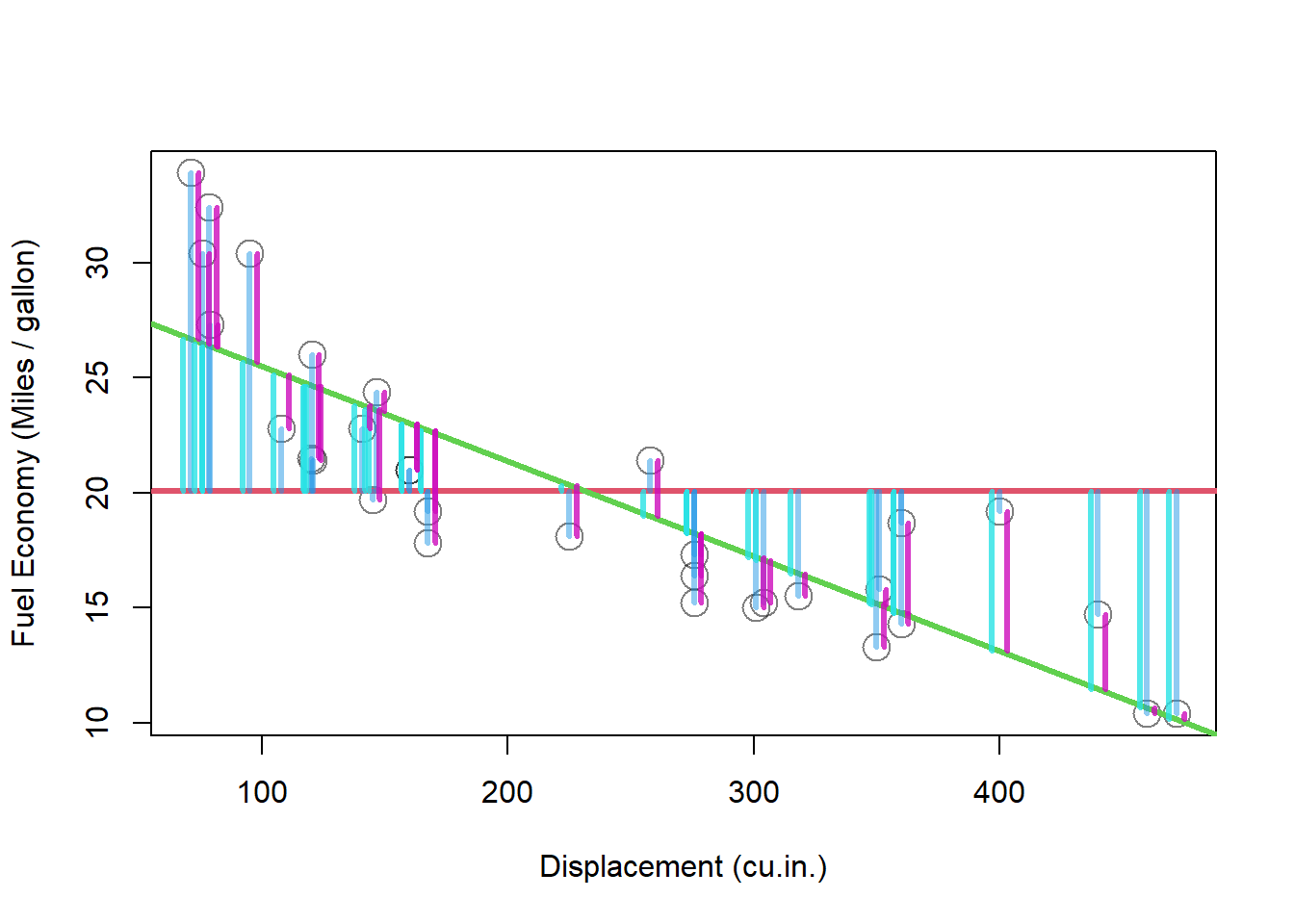
plot(mtcars$disp, mtcars$mpg, cex = 2, xlab= "Displacement (cu.in.)", ylab = "Fuel Economy (Miles / gallon)")
abline(h = mean(mtcars$mpg), col = 2, lwd = 3)
deviation_original <- mtcars$mpg - mean(mtcars$mpg)
segments(mtcars$disp, mtcars$mpg, mtcars$disp, mtcars$mpg - deviation_original, col = 4, lwd = 3)
排気量dispが少ないほど燃費mpgは高くなる傾向がありそうですが、ばらつきが結構あることがわかります。 青線が平均と実測値の差、つまり偏差 deviation となります。 偏差自体は符号が負(マイナス)になることがあるため、距離に表すために2乗してそれを足し合わせたものが偏差平方和 deviation sum of squares (\(SS\))となります。
次に、予測値の偏差平方和を求めます。 Rではlm関数で簡単に線形回帰ができます。 今回は、単純に線形回帰により予測値を求めます。
Call:
lm(formula = mpg ~ disp, data = mtcars)
Coefficients:
(Intercept) disp
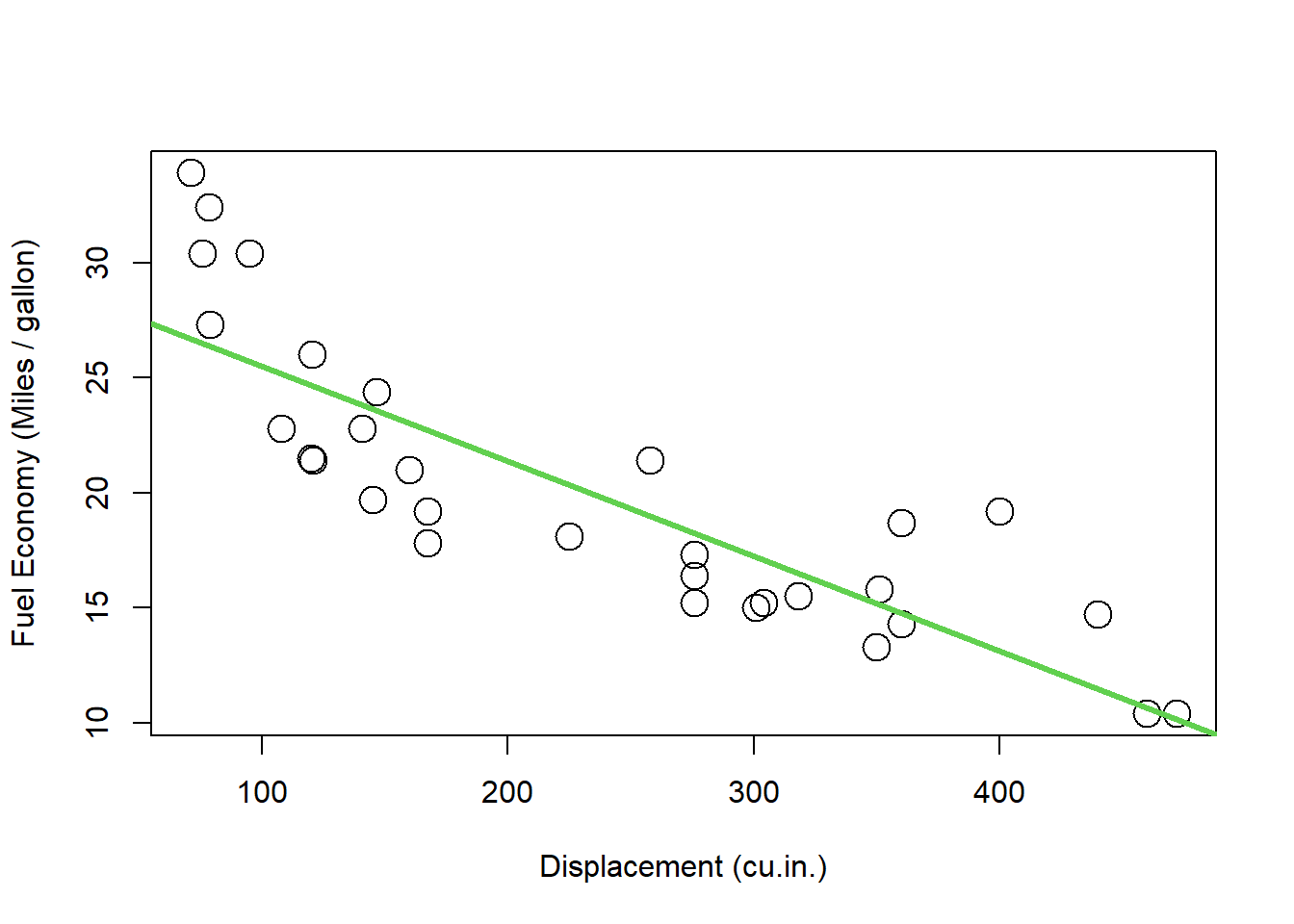
29.59985 -0.04122 回帰線をプロットに重ねてみます。
plot(mtcars$disp, mtcars$mpg, cex = 2, xlab = "Displacement (cu.in.)", ylab = "Fuel Economy (Miles / gallon)")
abline(model, col = 3, lwd = 3)
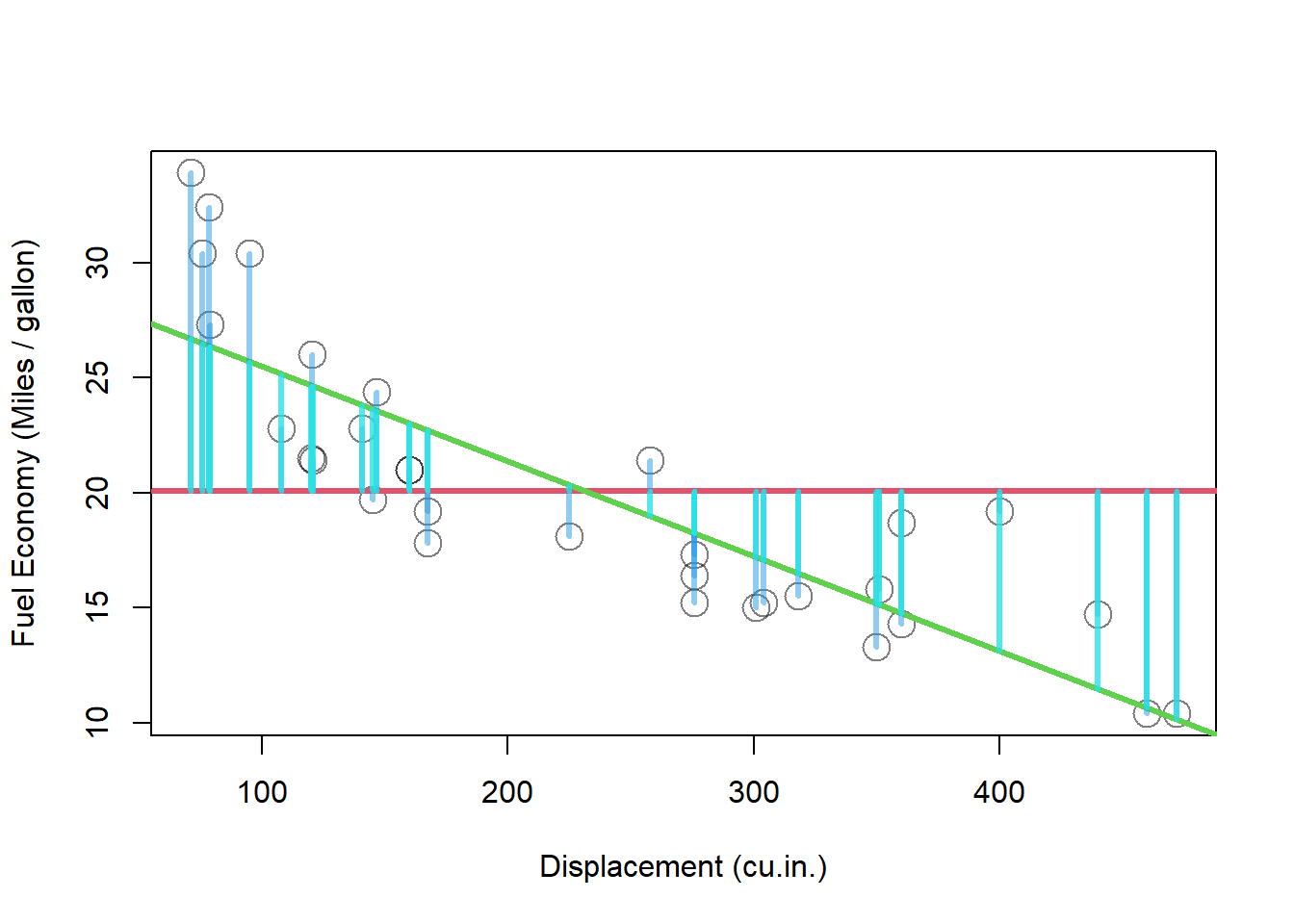
モデルから予測値を取り出し、偏差を可視化してみます。
plot(mtcars$disp, mtcars$mpg, cex = 2, xlab = "Displacement (cu.in.)", ylab = "Fuel Economy (Miles / gallon)", col = adjustcolor(1, alpha.f = 0.5))
abline(h = mean(mtcars$mpg), col = 2, lwd = 3)
deviation_model <- model$fitted.values - mean(mtcars$mpg)
abline(model, col = 3, lwd = 3)
segments(mtcars$disp, mtcars$mpg, mtcars$disp, mtcars$mpg - deviation_original, col = adjustcolor(4, alpha.f = 0.5), lwd = 3)
segments(mtcars$disp, model$fitted.values, mtcars$disp, model$fitted.values - deviation_model, col = adjustcolor(5, alpha.f = 0.8), lwd = 3)
全体的に偏差が小さくなっていることがわかります。 モデルの予測値の偏差平方和を算出してみます。
\(R^2\)を計算します。
\(R^2\)の算出式を再掲します。
\[ R^2 = \frac{予測値の偏差平方和}{実測値の偏差平方和} = \frac{SS_\mathrm{model}}{SS_\mathrm{original}} \]
モデルをsummary関数にいれることでも\(R^2\)を得ることができます。 自分で計算した値と同じになっていることを確認します。
解釈としては、モデルは全体のばらつきの71%を説明できているということになります。 今回で言えば、mpg(燃費)のばらつきはdisp(排気量)で71%を予測できるとも言えます。 逆に、残りの29%は別の要因によるものであると言えます。
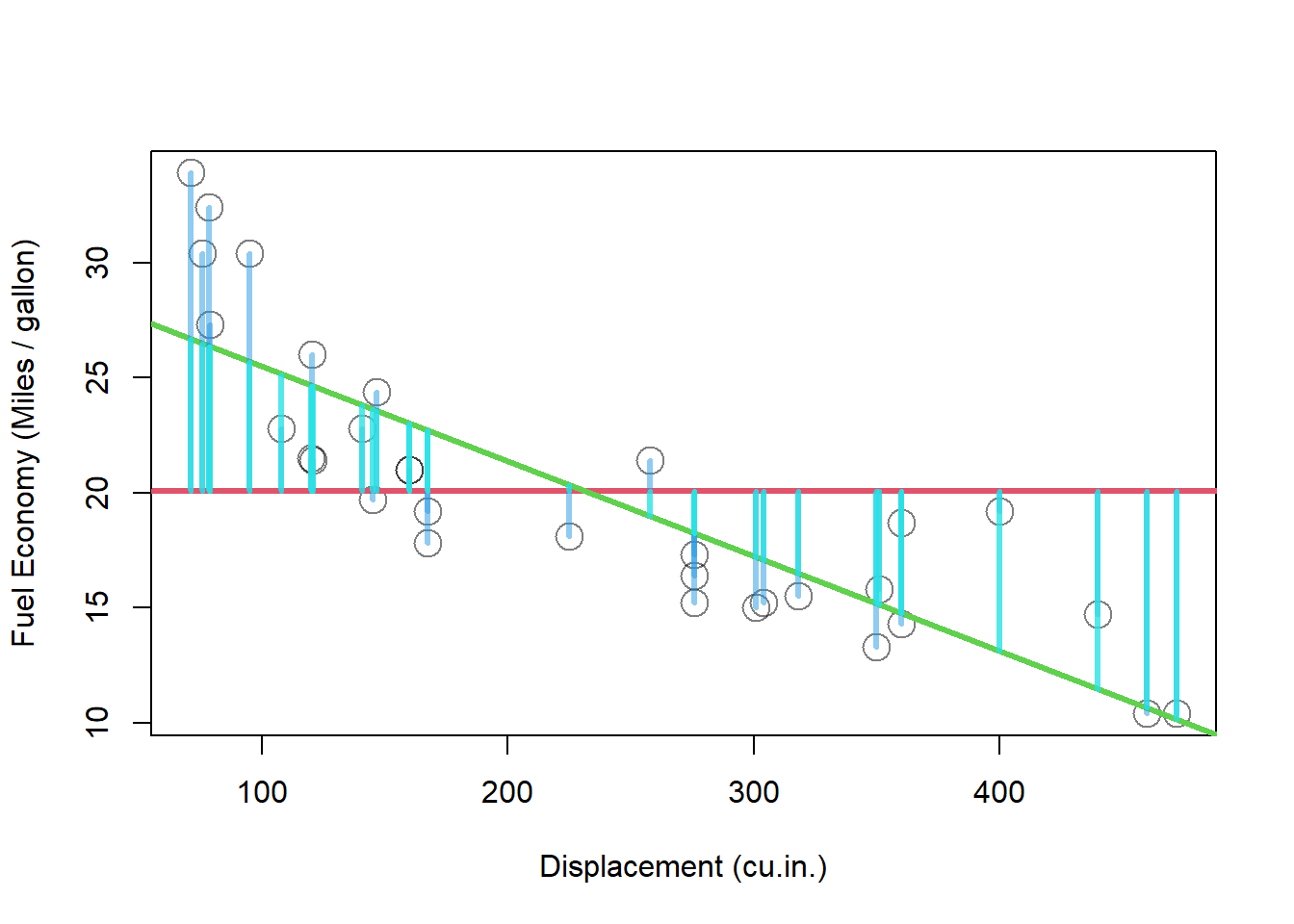
もう一つの\(R^2\)の算出方法として、残差を利用する方法があります。 今一度、元データとモデルの偏差のグラフを見てみます。
model <- lm(mpg ~ disp, data = mtcars)
plot(mtcars$disp, mtcars$mpg, cex = 2, xlab = "Displacement (cu.in.)", ylab = "Fuel Economy (Miles / gallon)", col = adjustcolor(1, alpha.f = 0.5))
abline(h = mean(mtcars$mpg), col = 2, lwd = 3)
deviation_model <- model$fitted.values - mean(mtcars$mpg)
abline(model, col = 3, lwd = 3)
segments(mtcars$disp, mtcars$mpg, mtcars$disp, mtcars$mpg - deviation_original, col = adjustcolor(4, alpha.f = 0.5), lwd = 3)
segments(mtcars$disp, model$fitted.values, mtcars$disp, model$fitted.values - deviation_model, col = adjustcolor(5, alpha.f = 0.8), lwd = 3)
モデルの偏差平方和は元データの偏差と重なっていますが、重なっていない残りの部分があることがわかります。 ここが残差 residualです。 残差はmodel$residualsもしくはresidual関数を用いてresidual(model)のように得ることができます。
Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive
-2.0054356 -2.0054356 -2.3486218 2.4336462
Hornet Sportabout Valiant Duster 360 Merc 240D
3.9375884 -2.2264528 -0.4624116 0.8464033
Merc 230 Merc 280 Merc 280C Merc 450SE
-0.9967659 -3.4922007 -4.8922007 -1.8327247
Merc 450SL Merc 450SLC Cadillac Fleetwood Lincoln Continental
-0.9327247 -3.0327247 0.2536819 -0.2408996
Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla
3.2347980 6.0437752 3.9201298 7.2305403
Toyota Corona Dodge Challenger AMC Javelin Camaro Z28
-3.1499188 -0.9934466 -1.8704583 -1.8745628
Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
6.0861932 0.9561397 1.3583242 4.7197032
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
0.6666524 -3.9236624 -2.1941036 -3.2128252 Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive
-2.0054356 -2.0054356 -2.3486218 2.4336462
Hornet Sportabout Valiant Duster 360 Merc 240D
3.9375884 -2.2264528 -0.4624116 0.8464033
Merc 230 Merc 280 Merc 280C Merc 450SE
-0.9967659 -3.4922007 -4.8922007 -1.8327247
Merc 450SL Merc 450SLC Cadillac Fleetwood Lincoln Continental
-0.9327247 -3.0327247 0.2536819 -0.2408996
Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla
3.2347980 6.0437752 3.9201298 7.2305403
Toyota Corona Dodge Challenger AMC Javelin Camaro Z28
-3.1499188 -0.9934466 -1.8704583 -1.8745628
Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa
6.0861932 0.9561397 1.3583242 4.7197032
Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E
0.6666524 -3.9236624 -2.1941036 -3.2128252 残差を加えて、先程のグラフをもう一度見てみます。 偏差や残差の棒を少しずらしてわかりやすく表示します。
model <- lm(mpg ~ disp, data = mtcars)
plot(mtcars$disp, mtcars$mpg, cex = 2, xlab = "Displacement (cu.in.)", ylab = "Fuel Economy (Miles / gallon)", col = adjustcolor(1, alpha.f = 0.5))
abline(h = mean(mtcars$mpg), col = 2, lwd = 3)
deviation_model <- model$fitted.values - mean(mtcars$mpg)
abline(model, col = 3, lwd = 3)
offset <- 3
segments(mtcars$disp, mtcars$mpg, mtcars$disp, mtcars$mpg - deviation_original, col = adjustcolor(4, alpha.f = 0.5), lwd = 3)
segments(mtcars$disp - offset, model$fitted.values, mtcars$disp - offset, model$fitted.values - deviation_model, col = adjustcolor(5, alpha.f = 0.8), lwd = 3)
segments(mtcars$disp + offset, model$fitted.values, mtcars$disp + offset, model$fitted.values + model$residuals, col = adjustcolor(6, alpha.f = 0.8), lwd = 3)
コードや図がやや複雑になってしまいましたが、この図から元データの偏差の絶対値合計 = モデルの偏差絶対値合計 + モデルの残差の絶対値合計となりそうだとわかります。
言い換えると、「元データの偏差平方和 = モデルの偏差平方和 + モデルの残差平方和」が成り立ちます。 実際に確かめてみます。
[1] 1126.047[1] 808.8885[1] 317.1587[1] -2.273737e-13丸め込みの影響などで完全に同じになっていませんが、大体おなじになっていることがわかります。
これらのことから、\(R^2\)の式について考えてみます。 元データの偏差平方和を\(SS_\mathrm{original}\)、モデルの偏差平方和を\(SS_\mathrm{model}\)とすると、\(R^2\)は以下の式になるのでした。
\[ R^2 = \frac{SS_\mathrm{model}}{SS_\mathrm{original}} \]
ここで、モデルの残差を平方和を\(SS_\mathrm{residual}\)とすると、 これらの3つの平方和の関係は以下のようになるのでした。
\[ SS_\mathrm{original} = SS_\mathrm{model} + SS_\mathrm{residual} \]
\(SS_\mathrm{model}\)について式を整理すると、以下のようになります。
\[ SS_\mathrm{model} = SS_\mathrm{original} - SS_\mathrm{residual} \]
これを、元の\(R^2\)の式に代入して整理します。
\[ \begin{align} R^2 &= \frac{SS_\mathrm{model}}{SS_\mathrm{original}} \\ &= \frac{SS_\mathrm{original} - SS_\mathrm{residual}}{SS_\mathrm{original}} \\ &= 1 - \frac{SS_\mathrm{residual}}{SS_\mathrm{original}} \end{align} \]
このことから、残差平方和を用いて\(R^2\)を導出できました。
元データの偏差平方和\(SS_\mathrm{original}\)はモデルで考えると、「切片だけのモデルの残差平方和」と言いかえることができます。
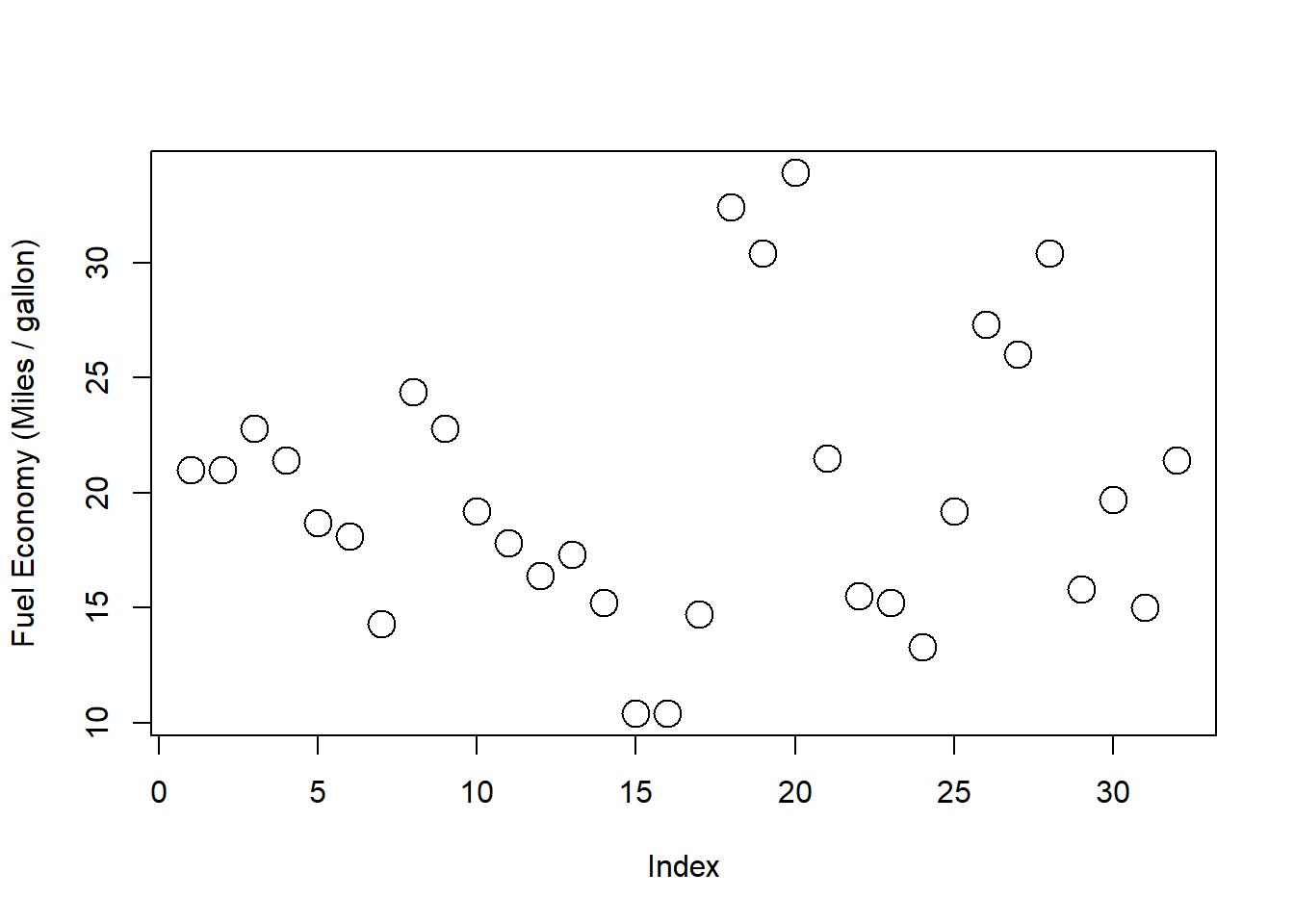
具体的にグラフで考えてみます。 x軸に変数を取らず、燃費mpgをプロットしてみます。 Rの場合、plot関数にベクトルを一つだけ渡すとx軸はIndexという名前になり、一変数だけをプロットできます。
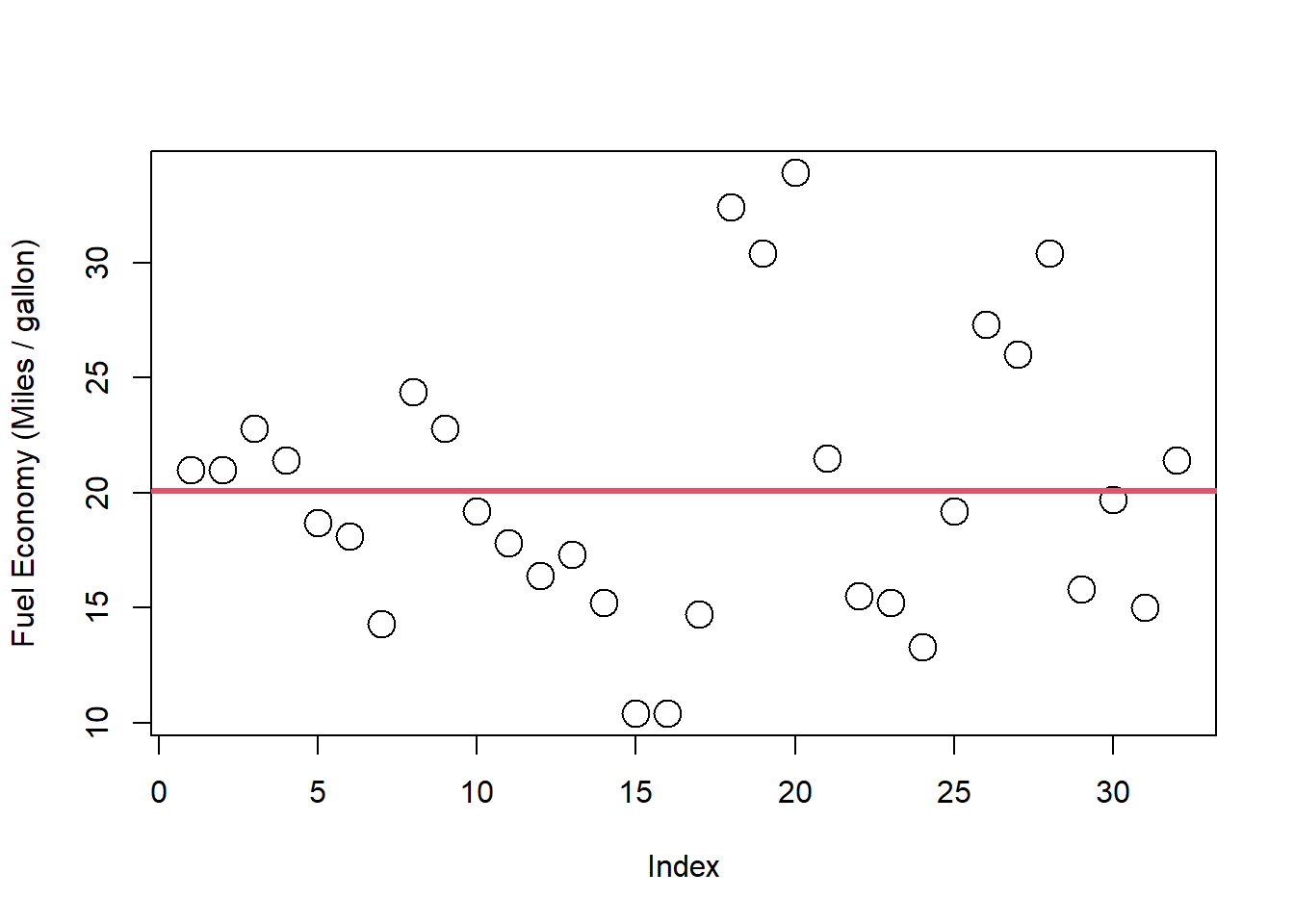
平均値に線を引いてみます。
plot(mtcars$mpg, ylab = "Fuel Economy (Miles / gallon)", cex = 2)
abline(h = mean(mtcars$mpg), col = 2, lwd =3)
平均値はそれぞれの点からの距離の合計値が最小になる値です。 証明は微分とかが必要になりそうなので省きますが、直感的に理解するとしたら、偏差の和が0になるため、平均値はそれぞれの値のばらつきが最小になる点であると考えることができます。
つまり、燃費mpgは、線形回帰で\(y = ax + b\)を当てはめると、一変数のため傾き\(a\)は0(横ばい)になり、切片\(b\)が平均値となります。
このことから、元データ、すなわち一変数のモデルを考えた場合、偏差平方和 = 残差平方和が成り立ちます。
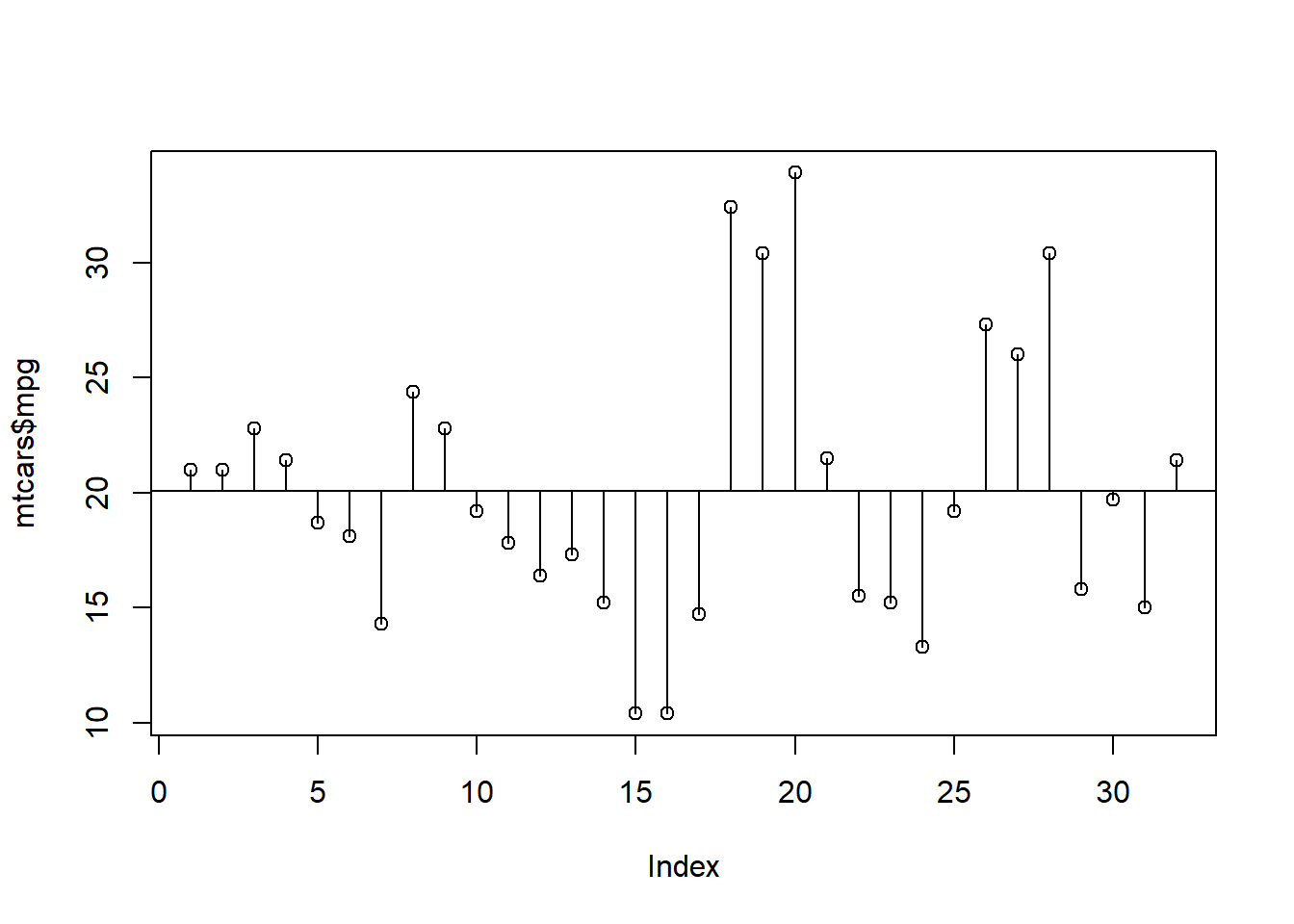
実際に切片だけのモデルも作成して考えてみます。 Rで切片だけのモデルを作成するには、説明変数に1とだけ書きます。
Call:
lm(formula = mpg ~ 1, data = mtcars)
Coefficients:
(Intercept)
20.09 出力がInterceps(切片)だけになっていることがわかります。 平均値とこの切片を比べます。
同じになっていることがわかります。
