Rでlmer関数を使って線形混合モデルを作成する

パッケージの読み込み

lmer関数はlme4パッケージに入っています。 まだインストールが済んでいなかったらinstall.packages関数でインストールします。

install.packages("lem4")

その後、library関数でパッケージを読み込みます。

library(lme4)

Loading required package: Matrix

使うデータセット

パッケージに入っている、sleepstudyというデータセットが練習として使えそうです。 パッケージを読み込んだ後であれば、そのままデータセット名で実行するだけで読み込めます。

sleepstudy

    Reaction Days Subject
1   249.5600    0     308
2   258.7047    1     308
3   250.8006    2     308
4   321.4398    3     308
5   356.8519    4     308
6   414.6901    5     308
7   382.2038    6     308
8   290.1486    7     308
9   430.5853    8     308
10  466.3535    9     308
11  222.7339    0     309
12  205.2658    1     309
13  202.9778    2     309
14  204.7070    3     309
15  207.7161    4     309
16  215.9618    5     309
17  213.6303    6     309
18  217.7272    7     309
19  224.2957    8     309
20  237.3142    9     309
21  199.0539    0     310
22  194.3322    1     310
23  234.3200    2     310
24  232.8416    3     310
25  229.3074    4     310
26  220.4579    5     310
27  235.4208    6     310
28  255.7511    7     310
29  261.0125    8     310
30  247.5153    9     310
31  321.5426    0     330
32  300.4002    1     330
33  283.8565    2     330
34  285.1330    3     330
35  285.7973    4     330
36  297.5855    5     330
37  280.2396    6     330
38  318.2613    7     330
39  305.3495    8     330
40  354.0487    9     330
41  287.6079    0     331
42  285.0000    1     331
43  301.8206    2     331
44  320.1153    3     331
45  316.2773    4     331
46  293.3187    5     331
47  290.0750    6     331
48  334.8177    7     331
49  293.7469    8     331
50  371.5811    9     331
51  234.8606    0     332
52  242.8118    1     332
53  272.9613    2     332
54  309.7688    3     332
55  317.4629    4     332
56  309.9976    5     332
57  454.1619    6     332
58  346.8311    7     332
59  330.3003    8     332
60  253.8644    9     332
61  283.8424    0     333
62  289.5550    1     333
63  276.7693    2     333
64  299.8097    3     333
65  297.1710    4     333
66  338.1665    5     333
67  332.0265    6     333
68  348.8399    7     333
69  333.3600    8     333
70  362.0428    9     333
71  265.4731    0     334
72  276.2012    1     334
73  243.3647    2     334
74  254.6723    3     334
75  279.0244    4     334
76  284.1912    5     334
77  305.5248    6     334
78  331.5229    7     334
79  335.7469    8     334
80  377.2990    9     334
81  241.6083    0     335
82  273.9472    1     335
83  254.4907    2     335
84  270.8021    3     335
85  251.4519    4     335
86  254.6362    5     335
87  245.4523    6     335
88  235.3110    7     335
89  235.7541    8     335
90  237.2466    9     335
91  312.3666    0     337
92  313.8058    1     337
93  291.6112    2     337
94  346.1222    3     337
95  365.7324    4     337
96  391.8385    5     337
97  404.2601    6     337
98  416.6923    7     337
99  455.8643    8     337
100 458.9167    9     337
101 236.1032    0     349
102 230.3167    1     349
103 238.9256    2     349
104 254.9220    3     349
105 250.7103    4     349
106 269.7744    5     349
107 281.5648    6     349
108 308.1020    7     349
109 336.2806    8     349
110 351.6451    9     349
111 256.2968    0     350
112 243.4543    1     350
113 256.2046    2     350
114 255.5271    3     350
115 268.9165    4     350
116 329.7247    5     350
117 379.4445    6     350
118 362.9184    7     350
119 394.4872    8     350
120 389.0527    9     350
121 250.5265    0     351
122 300.0576    1     351
123 269.8939    2     351
124 280.5891    3     351
125 271.8274    4     351
126 304.6336    5     351
127 287.7466    6     351
128 266.5955    7     351
129 321.5418    8     351
130 347.5655    9     351
131 221.6771    0     352
132 298.1939    1     352
133 326.8785    2     352
134 346.8555    3     352
135 348.7402    4     352
136 352.8287    5     352
137 354.4266    6     352
138 360.4326    7     352
139 375.6406    8     352
140 388.5417    9     352
141 271.9235    0     369
142 268.4369    1     369
143 257.2424    2     369
144 277.6566    3     369
145 314.8222    4     369
146 317.2135    5     369
147 298.1353    6     369
148 348.1229    7     369
149 340.2800    8     369
150 366.5131    9     369
151 225.2640    0     370
152 234.5235    1     370
153 238.9008    2     370
154 240.4730    3     370
155 267.5373    4     370
156 344.1937    5     370
157 281.1481    6     370
158 347.5855    7     370
159 365.1630    8     370
160 372.2288    9     370
161 269.8804    0     371
162 272.4428    1     371
163 277.8989    2     371
164 281.7895    3     371
165 279.1705    4     371
166 284.5120    5     371
167 259.2658    6     371
168 304.6306    7     371
169 350.7807    8     371
170 369.4692    9     371
171 269.4117    0     372
172 273.4740    1     372
173 297.5968    2     372
174 310.6316    3     372
175 287.1726    4     372
176 329.6076    5     372
177 334.4818    6     372
178 343.2199    7     372
179 369.1417    8     372
180 364.1236    9     372

180行3列のデータフレームです。 説明によると、「睡眠不足研究における応答時間」のデータということです。 どうやら、被験者を睡眠不足にして、それによって何かへの応答(反応)速度がどう変わるかを見ているようです。 * Reaction: 平均応答時間 (ms) * Days: 睡眠不足の日数 * Subject: 被験者番号 (18人いる)

str関数を用いることで構造が簡単にわかります。

str(sleepstudy)

'data.frame':   180 obs. of  3 variables:
 $ Reaction: num  250 259 251 321 357 ...
 $ Days    : num  0 1 2 3 4 5 6 7 8 9 ...
 $ Subject : Factor w/ 18 levels "308","309","310",..: 1 1 1 1 1 1 1 1 1 1 ...

データの可視化

とりあえず睡眠不足の日数に対して応答速度がどのように変化するかプロットします。 色分けは被験者番号ごとにします。

plot(sleepstudy$Days, sleepstudy$Reaction, col = sleepstudy$Subject, xlab = "Days", ylab = "Reaction Time (ms)", yaxt = "n")
axis(2, las = 2)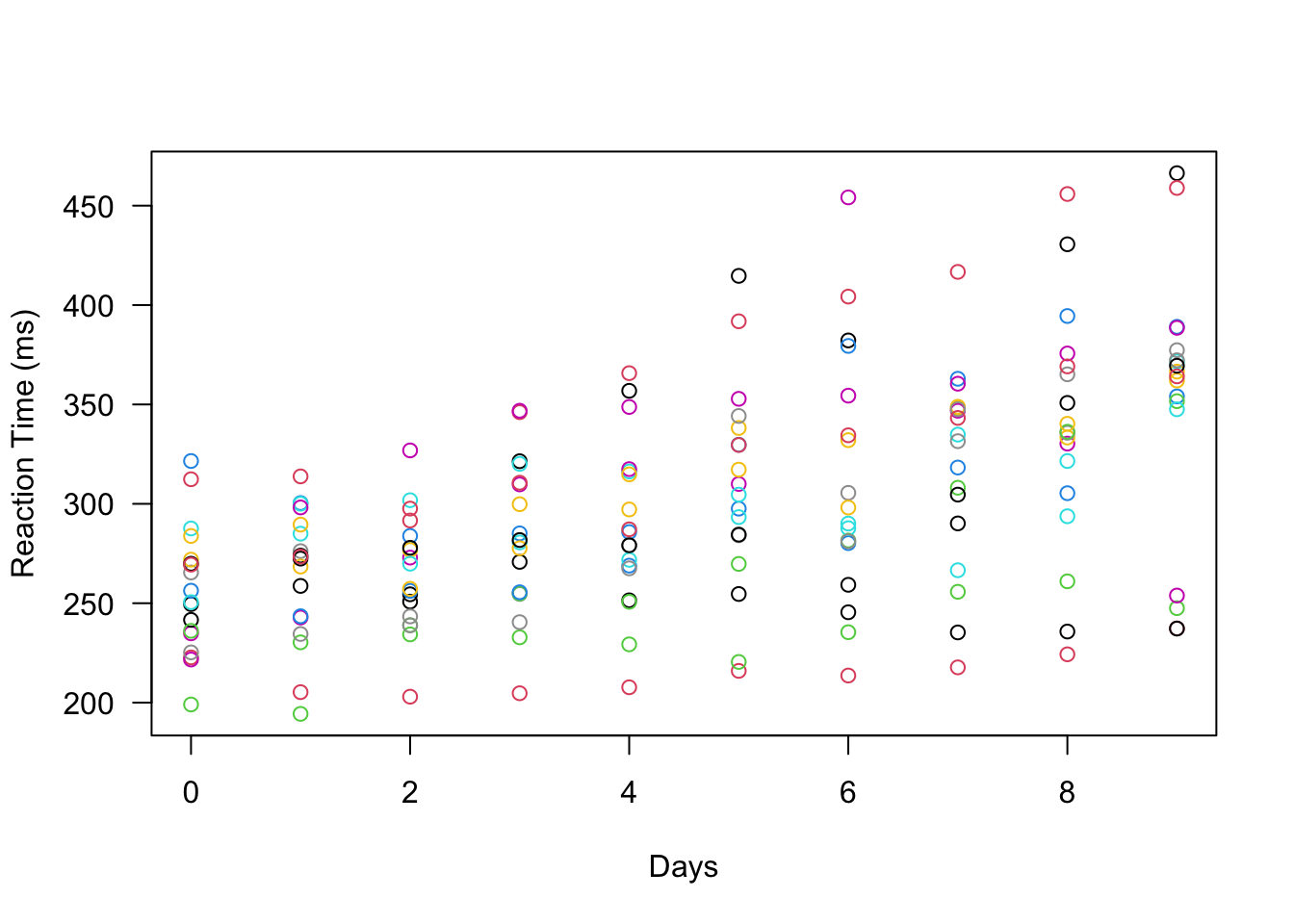

被験者ごとに傾きや切片が異なっていそうとわかります。

線形混合モデルの作成

被験者ごとに傾きや切片が異なっているということで、被験者をランダム効果に入れることで個人差の影響と全体の傾向を分けることができます。 睡眠不足の日数に対し、スタート時点での応答速度(切片)と睡眠不足の影響(傾き)がそれぞれ人によって異なるとすると、(Days | Subject)とすれば切片と傾きをランダム効果にいれることができるようです。 lmer関数でモデルを作成し、そのモデルをsummary関数にいれることでわかりやすく結果を得ることができます。

model <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)
result <- summary(model)
result

Linear mixed model fit by REML ['lmerMod']
Formula: Reaction ~ Days + (Days | Subject)
   Data: sleepstudy

REML criterion at convergence: 1743.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.9536 -0.4634  0.0231  0.4634  5.1793 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 Subject  (Intercept) 612.10   24.741       
          Days         35.07    5.922   0.07
 Residual             654.94   25.592       
Number of obs: 180, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error t value
(Intercept)  251.405      6.825  36.838
Days          10.467      1.546   6.771

Correlation of Fixed Effects:
     (Intr)
Days -0.138

ばらつきの割合を見る

共分散行列の対角要素に切片や変数の分散が入っています。 また、残差の標準偏差はsigmaという名前で入っているので、それを二乗することで残差の分散を取り出します。

var_intercept <- result$varcor$Subject[1, 1] # 切片の分散 variance
var_days <- result$varcor$Subject[2, 2] # Daysのvariance
var_residual <- result$sigma^2 # 残差のvariance
var_sum <-  sum(var_intercept, var_days, var_residual)
ratio_var_intercept <- var_intercept / var_sum
ratio_var_days <- var_days / var_sum
ratio_var_residual <- var_residual / var_sum

切片、傾き、残差のばらつきがそれぞれ得られます。

print(paste("切片のばらつき:", round(ratio_var_intercept * 100, 1), "%"))

[1] "切片のばらつき: 47 %"

print(paste("傾きのばらつき:", round(ratio_var_days * 100, 1), "%"))

[1] "傾きのばらつき: 2.7 %"

print(paste("残差のばらつき:", round(ratio_var_residual * 100, 1), "%"))

[1] "残差のばらつき: 50.3 %"

予測線を描く

predict関数に作成したモデルを入れることで、簡単にそれぞれの点の予測値を計算してくれます。

plot(sleepstudy$Days, sleepstudy$Reaction, col = sleepstudy$Subject, xlab = "Days", ylab = "Reaction Time (ms)", yaxt = "n", main = "Original")
axis(2, las = 2)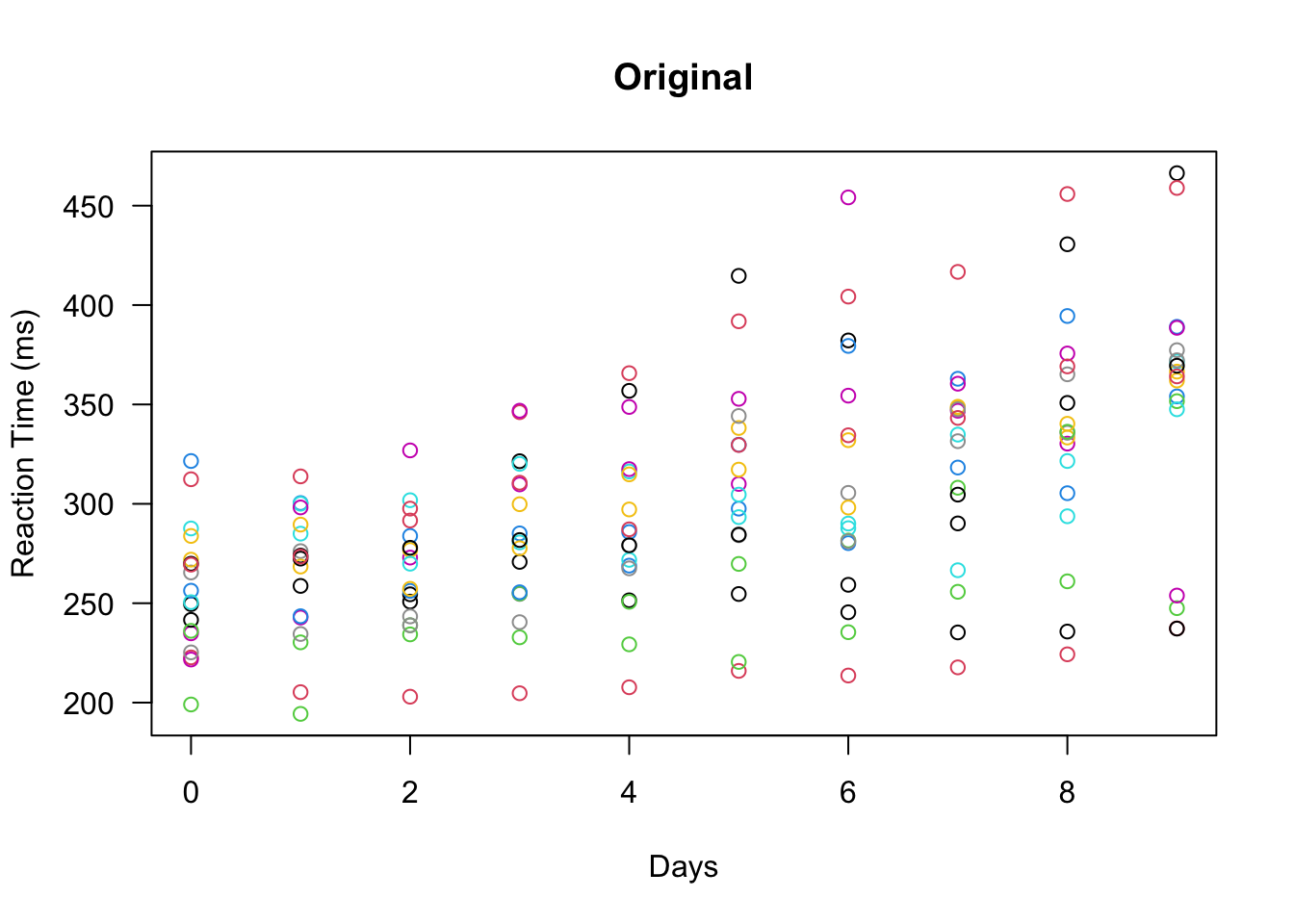

predictions <- predict(model)
plot(sleepstudy$Days, predictions, col = sleepstudy$Subject, xlab = "Days", ylab = "Reaction Time (ms)", yaxt = "n", main = "Prediction")
axis(2, las = 2)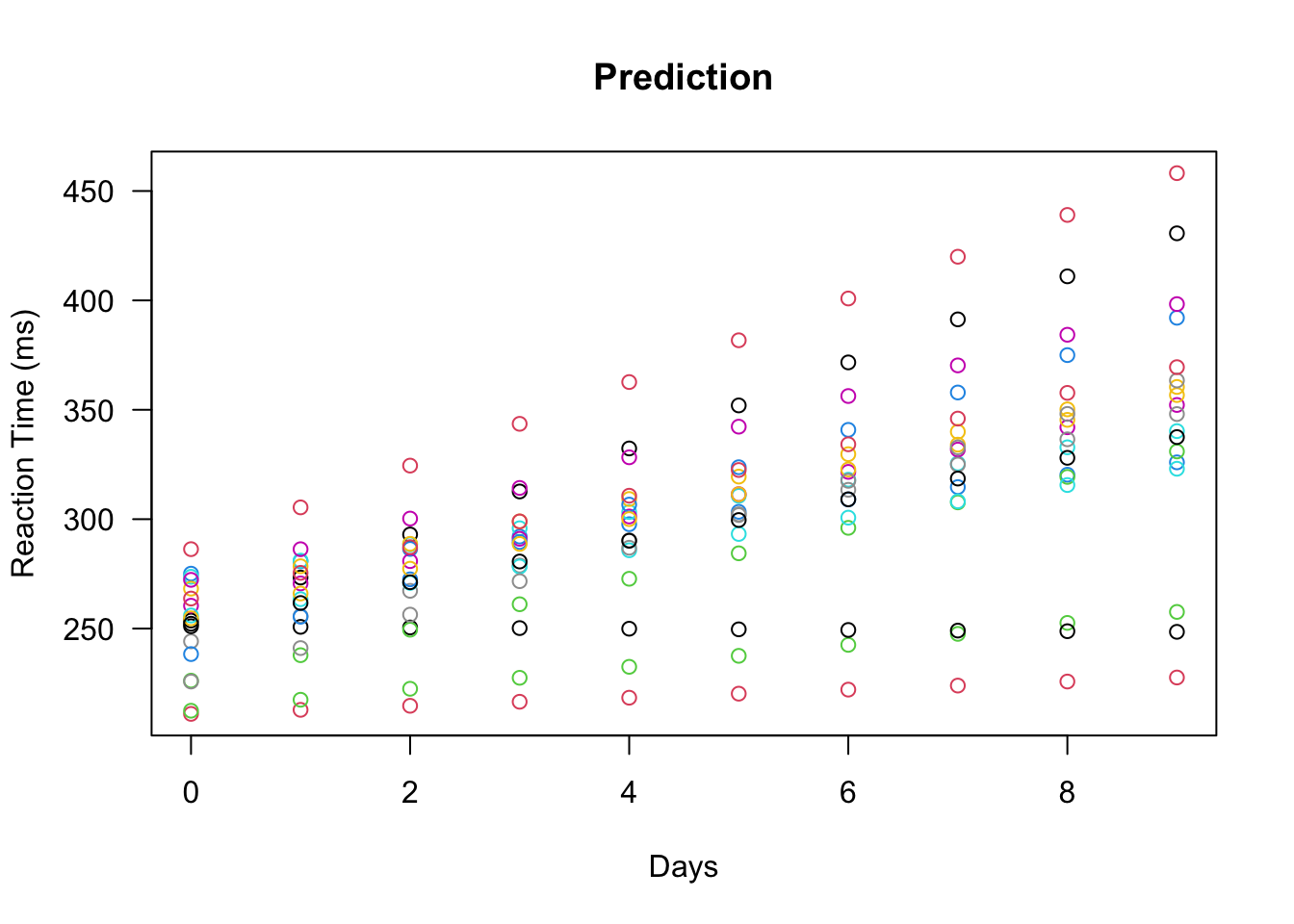

残差について

summary(model)で得られたresultオブジェクトにはresidualsという名前で残差が入っています。 しかし、これはそのままの残差ではなく、スケール残差 scaled residualsというものになります。 scaled residualsは以下の式で計算されます。

\[ \mathrm{scaled \ residuals} = \frac{\mathrm{residuals}}{\mathrm{SD(residuals)}} \]

SDは標準偏差 standard deviationです。 redisuals自体は、実際のデータ - 予測値で得られます。 予測値自体は先ほどpredict(model)で得られた値です。

「実測データ-予測値」とモデルから得られる残差が一致することを確かめます。

sleepstudy$Reaction - predictions

           1            2            3            4            5            6 
  -4.1036558  -14.6252175  -42.1955792    8.7773590   24.5231973   62.6951356 
           7            8            9           10           11           12 
  10.5425739 -101.1788879   19.5915504   35.6934887   11.7275332   -7.5881721 
          13           14           15           16           17           18 
 -11.7237775  -11.8421828  -10.6806881   -4.2825935   -8.4616988   -6.2124042 
          19           20           21           22           23           24 
  -1.4915095    9.6793851  -13.3907959  -23.1309254   11.8384451    5.3416156 
          25           26           27           28           29           30 
  -3.2110139  -17.0789433   -7.1344728    8.1773977    8.4203682  -10.0952613 
          31           32           33           34           35           36 
  46.4468756   19.6515399   -2.5450957   -6.9215313  -11.9101670   -5.7749026 
          37           38           39           40           41           42 
 -28.7737382    3.5950261  -14.9697095   28.0765548   13.9424826    3.9372082 
          43           44           45           46           47           48 
  13.3604339   24.2577595   13.0223852  -17.3335892  -27.9746635    9.3706621 
          49           50           51           52           53           54 
 -39.0975122   31.3393134  -25.5840727  -27.8279817   -7.8735907   18.7388004 
          55           56           57           58           59           60 
  16.2377914   -1.4226176  132.5465735   15.0206645  -11.7052445  -98.3362534 
          61           62           63           64           65           66 
  15.5967865   11.0657367  -11.9636132    0.8331369  -12.0492130   18.7026372 
          67           68           69           70           71           72 
   2.3189873    8.8887374  -16.8348125    1.6043376   21.3006103   20.4868426 
          73           74           75           76           77           78 
 -23.8915250  -24.1257926  -11.3155602  -17.6906278   -7.8988954    6.5573370 
          79           80           81           82           83           84 
  -0.7605306   29.2497018   -9.4631364   23.1606428    3.9890220   20.5853012 
          85           86           87           88           89           90 
   1.5199804    4.9891597   -3.9098611  -13.7662819  -13.0383027  -11.2609235 
          91           92           93           94           95           96 
  26.0710083    8.4146572  -32.8754939    2.5399550    3.0546039   10.0651527 
          97           98           99          100          101          102 
   3.3912016   -3.2721495   16.8042994    0.7611483    9.9083238   -7.5188944 
         103          104          105          106          107          108 
 -10.5507125   -6.1950306  -22.0474488  -14.6240669  -14.4743850    0.4220968 
         109          110          111          112          113          114 
  16.9599787   20.6837606   17.9617293  -11.9622745  -16.2934782  -34.0524820 
         115          116          117          118          119          120 
 -37.7445858    5.9821105   38.6204067    5.0128029   19.5000992   -3.0159046 
         121          122          123          124          125          126 
  -5.4564690   36.6226071   -0.9931168    2.2500593  -13.9636645   11.3905116 
         127          128          129          130          131          132 
 -12.9485123  -41.5516362    5.9426399   24.5143161  -50.5916830   11.9218299 
         133          134          135          136          137          138 
  26.6031428   32.5768557   20.4582686   10.5434816   -1.8619055   -9.8591926 
         139          140          141          142          143          144 
  -8.6544797   -9.7566668   17.2429295    2.4168287  -20.1171721  -11.0424730 
         145          146          147          148          149          150 
  14.7836262    5.8354254  -24.5822755   14.0658237   -5.1165771    9.7770220 
         151          152          153          154          155          156 
  -0.5281055   -6.5583765  -17.4708474  -31.1884183  -19.4138892   41.9527399 
         157          158          159          160          161          162 
 -36.3826310   14.7649981   17.0527272    8.8287562   17.6682491   10.7515193 
         163          164          165          166          167          168 
   6.7284896    1.1399599  -10.9581699  -15.0957996  -49.8211294  -13.9354591 
         169          170          171          172          173          174 
  22.7355112   31.9448814    5.6920030   -1.9970050   10.3744870   11.6579789 
         175          176          177          178          179          180 
 -23.5523291    7.1313629    0.2542548   -2.7589532   11.4115388   -5.3578693 

result$residuals * result$sigma

           1            2            3            4            5            6 
  -4.1036558  -14.6252175  -42.1955792    8.7773590   24.5231973   62.6951356 
           7            8            9           10           11           12 
  10.5425739 -101.1788879   19.5915504   35.6934887   11.7275332   -7.5881721 
          13           14           15           16           17           18 
 -11.7237775  -11.8421828  -10.6806881   -4.2825935   -8.4616988   -6.2124042 
          19           20           21           22           23           24 
  -1.4915095    9.6793851  -13.3907959  -23.1309254   11.8384451    5.3416156 
          25           26           27           28           29           30 
  -3.2110139  -17.0789433   -7.1344728    8.1773977    8.4203682  -10.0952613 
          31           32           33           34           35           36 
  46.4468756   19.6515399   -2.5450957   -6.9215313  -11.9101670   -5.7749026 
          37           38           39           40           41           42 
 -28.7737382    3.5950261  -14.9697095   28.0765548   13.9424826    3.9372082 
          43           44           45           46           47           48 
  13.3604339   24.2577595   13.0223852  -17.3335892  -27.9746635    9.3706621 
          49           50           51           52           53           54 
 -39.0975122   31.3393134  -25.5840727  -27.8279817   -7.8735907   18.7388004 
          55           56           57           58           59           60 
  16.2377914   -1.4226176  132.5465735   15.0206645  -11.7052445  -98.3362534 
          61           62           63           64           65           66 
  15.5967865   11.0657367  -11.9636132    0.8331369  -12.0492130   18.7026372 
          67           68           69           70           71           72 
   2.3189873    8.8887374  -16.8348125    1.6043376   21.3006103   20.4868426 
          73           74           75           76           77           78 
 -23.8915250  -24.1257926  -11.3155602  -17.6906278   -7.8988954    6.5573370 
          79           80           81           82           83           84 
  -0.7605306   29.2497018   -9.4631364   23.1606428    3.9890220   20.5853012 
          85           86           87           88           89           90 
   1.5199804    4.9891597   -3.9098611  -13.7662819  -13.0383027  -11.2609235 
          91           92           93           94           95           96 
  26.0710083    8.4146572  -32.8754939    2.5399550    3.0546039   10.0651527 
          97           98           99          100          101          102 
   3.3912016   -3.2721495   16.8042994    0.7611483    9.9083238   -7.5188944 
         103          104          105          106          107          108 
 -10.5507125   -6.1950306  -22.0474488  -14.6240669  -14.4743850    0.4220968 
         109          110          111          112          113          114 
  16.9599787   20.6837606   17.9617293  -11.9622745  -16.2934782  -34.0524820 
         115          116          117          118          119          120 
 -37.7445858    5.9821105   38.6204067    5.0128029   19.5000992   -3.0159046 
         121          122          123          124          125          126 
  -5.4564690   36.6226071   -0.9931168    2.2500593  -13.9636645   11.3905116 
         127          128          129          130          131          132 
 -12.9485123  -41.5516362    5.9426399   24.5143161  -50.5916830   11.9218299 
         133          134          135          136          137          138 
  26.6031428   32.5768557   20.4582686   10.5434816   -1.8619055   -9.8591926 
         139          140          141          142          143          144 
  -8.6544797   -9.7566668   17.2429295    2.4168287  -20.1171721  -11.0424730 
         145          146          147          148          149          150 
  14.7836262    5.8354254  -24.5822755   14.0658237   -5.1165771    9.7770220 
         151          152          153          154          155          156 
  -0.5281055   -6.5583765  -17.4708474  -31.1884183  -19.4138892   41.9527399 
         157          158          159          160          161          162 
 -36.3826310   14.7649981   17.0527272    8.8287562   17.6682491   10.7515193 
         163          164          165          166          167          168 
   6.7284896    1.1399599  -10.9581699  -15.0957996  -49.8211294  -13.9354591 
         169          170          171          172          173          174 
  22.7355112   31.9448814    5.6920030   -1.9970050   10.3744870   11.6579789 
         175          176          177          178          179          180 
 -23.5523291    7.1313629    0.2542548   -2.7589532   11.4115388   -5.3578693 

一致していますね。

残差の可視化

残差を可視化してみます。 わかりやすさのために、最初の10点について見てみます。 ここでは、prediction(model)で得られた値でなく、モデルから得られる残差でプロットします。

residuals <- result$residuals * result$sigma
plot(sleepstudy$Days[1:10], sleepstudy$Reaction[1:10], col = 1, xlab = "Days", ylab = "Reaction Time (ms)", yaxt = "n")
axis(2, las = 2)
points(sleepstudy$Days[1:10], sleepstudy$Reaction[1:10] - residuals[1:10], col = 2)
segments(x0 = sleepstudy$Days[1:10], y0 = sleepstudy$Reaction[1:10], x1 = sleepstudy$Days[1:10], y1 = sleepstudy$Reaction[1:10] - residuals[1:10], col = 3)
legend("topleft", legend = c("Original", "Prediction", "Residuals"), col = 1:3, pch = c(1, 1, NA), lty = c(NA, NA, 1))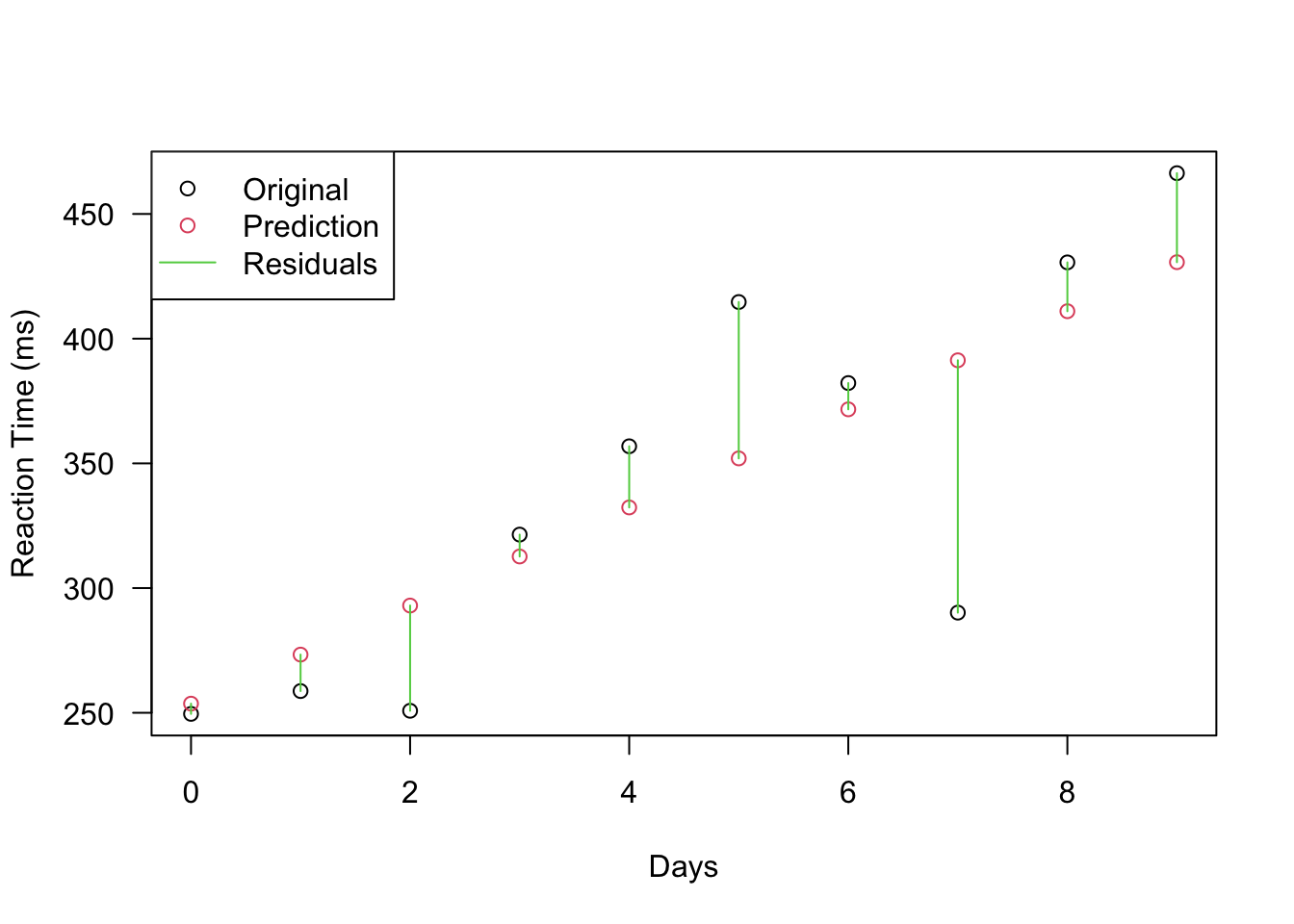

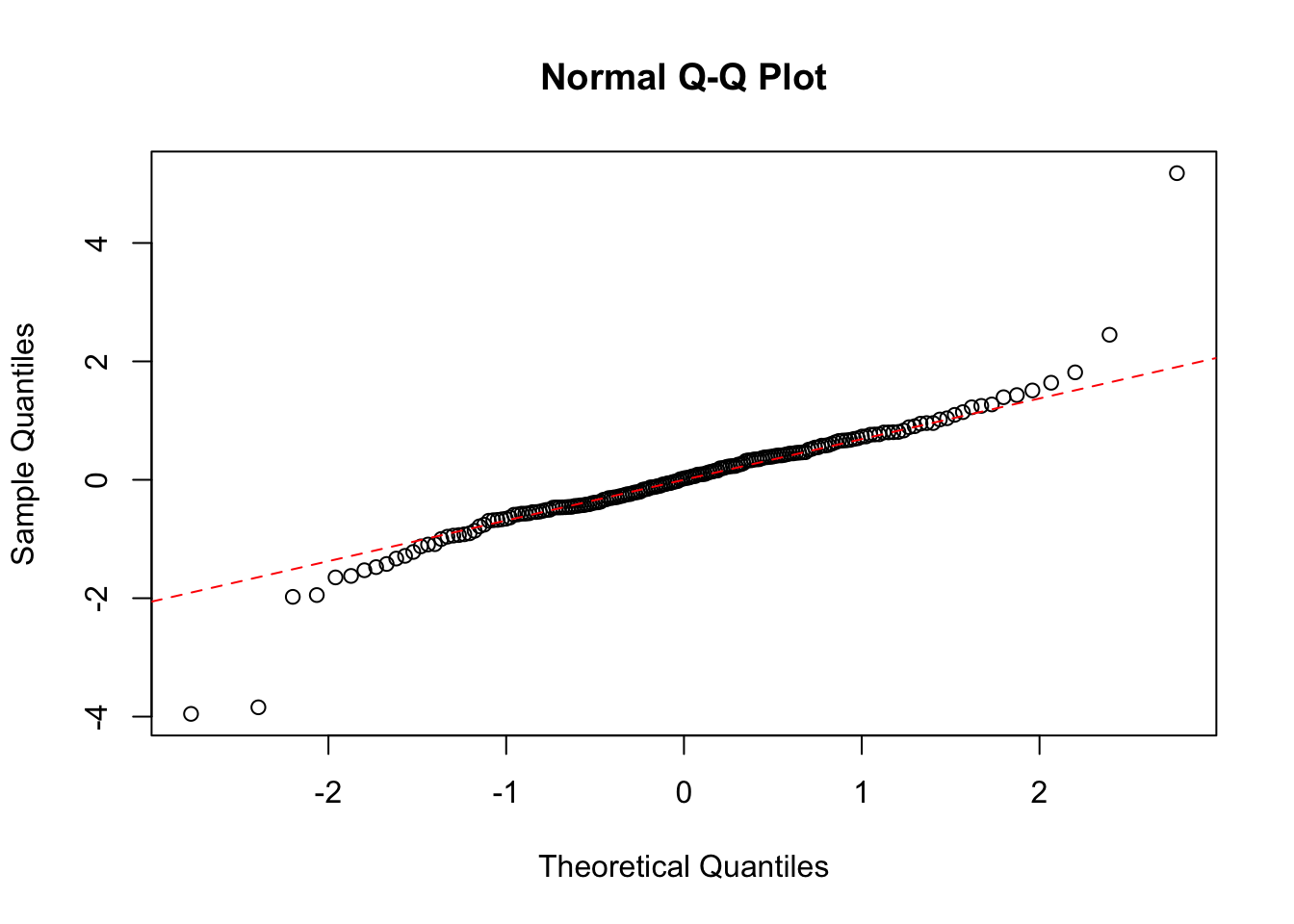
残差の正規性を確認する

Q-Qプロットを作成するには、qqnormとqqlineが有用です。 Q-Qプロットの意味については今回は掘り下げません。

qqnorm(result$residuals)
qqline(result$residuals, col = "red", lty = 2)